Γράφει ο Κωνσταντίνος Τσακιρίδης: Αναλυτής Ποδοσφαίρου
Football Performance Video and Data Αnalyst της ΠΑΕ ΠΙΕΡΙΚΟΣ 1961

Το Σύγχρονο Ποδόσφαιρο συναντάει την Επιστήμη των Μαθηματικών

Τι σχέση έχουν τα μαθηματικά με το ποδόσφαιρο; «Μια σχέση που θα κάνει τους ανυποψίαστους να εκπλαγούν και τους υποψιασμένους να σιγουρευτούν». Σε μια εποχή όπου το επαγγελματικό ποδόσφαιρο δεν είναι μόνο ζήτημα ταλέντου, τύχης και πολλών δισεκατομμυρίων, η επιστήμη αναγνωρίζεται ως το πιο χρήσιμο «εργαλείο» για την απόδοση ομάδων και ποδοσφαιριστών.

Πώς παίζουν οι μεγάλες ομάδες;

Ποιατακτική ακολουθούν οι διάσημοι παίκτες; Πού κρύβεται η ομορφιά του «ολοκληρωτικού ποδοσφαίρου»;

Οι ρίζες του total football βρίσκονται έξω από το ποδόσφαιρο. Η γοητεία του κρύβεται στην αρχιτεκτονική, τη γεωμετρία και στην ιδέα του μεγάλου μαθηματικού Ανρί Πουανκαρέ περί ευμετάβλητου χώρου. Από την αεροδυναμική της μπάλας, τονρόλο των παπουτσιών στα φαλτσαριστά σουτ, την ψυχολογία των ποδοσφαιριστώνστην διαδικασία των πέναλτι, τις αναλυτικές μετρήσεις και την παρακολούθηση τωνδεικτών που αφορούν στην εργοφυσιολογία των ποδοσφαιριστών, μέχρι την εξαντλητική μαθηματική ανάλυση των δυνατοτήτων που προσφέρουν τα αγωνιστικάσυστήματα, οι προπονητές έχουν αποκτήσει για τις δυνατότητες του παιχνιδιού, μιαγνώση που ολοένα διευρύνεται.

Μια γνώση στην οποία δεν έχουν πρόσβαση οι δημοσιογράφοι και οι φίλαθλοι και παρ’ όλα αυτά κρίνουν με απόλυτο τρόπο, τόσο το παιχνίδι όσο και τους ποδοσφαιριστές. Χωρούν τα Μαθηματικά στο ποδόσφαιρο; Και αν χωρούν, το κάνουν καλύτερο ή χειρότερο;

Μην ξεχνάμε ότι είναι ένα άθλημα που έχει φτιαχτεί για να μην μπαίνουν πολλά γκολ και να μην κερδίζει πάντα ο καλύτερος… Η ανάλυση 300.000 παιχνιδιών από διάφορα ομαδικά αθλήματα- μπάσκετ, μπέιζμπολ, χόκεϊ στον πάγο- έδειξε ότι το
ποδόσφαιρο είναι το πιο απρόβλεπτο απ ́ όλα σε ό,τι αφορά τα αποτελέσματα.

Πώς κυλά η (μπάλα) Jabulani
Η καινούρια μπάλα, η Jabulani (σημαίνει «να το γιορτάσουμε» στη γλώσσα των Ζουλού, σημαντική φυλή της Νοτιοαφρικής), με τα ένδεκα χρώματα για τις ένδεκα πιο πολυπληθείς φυλές που κατοικούν, στο κράτος της διοργανώτριας χώρας Νότιας Αφρικής, άρχισε να κυλάει στα γήπεδα. Σχεδιάστηκε, δοκιμάστηκε, κρίθηκε και επικρίθηκε. Είναι πάντως ένα ακόμη προϊόν
επιστημονικής έρευνας σε σχέση με τη συμπεριφορά διάφορων υλικών και δοκιμών σε αεροσήραγγες.

Μία ακόμη προσπάθεια οι νόμοι της Φυσικής να παίξουν κάποιο ρόλο στη διαμόρφωση του δημοφιλέστερου αθλήματος στον κόσμο. Μόνο που η επιστήμη εξ ορισμού έχει σκοπό να κάνει τα πράγματα γύρω μας περισσότερο προβλέψιμα, ενώ η γοητεία του ποδοσφαίρου είναι το ότι σε διοργανώσεις όπως το Μουντιάλ διάφοροι παράγοντες το κάνουν απρόβλεπτο. Αρα, πιο ενδιαφέρον.

Και η καινούρια μπάλα, για να μη μιλούμε έτσι στον αέρα, δεν ξεφεύγει από τα παραπάνω. Οπως παραπονέθηκαν πιο πολύ οι τερματοφύλακες, τους έρχεται με ανυπόφορη ταχύτητα. Και αυτό έχει την επιστημονική του εξήγηση. Διότι μέσα στην αεροσήραγγα, όπου δοκιμάζεται πλέον η κάθε μπάλα, αποδείχθηκε ότι καθώς κινείται στον αέρα και τον μετατοπίζει στα πλάγια για να περάσει εκείνη, στο πίσω μέρος της δημιουργούνται στρόβιλοι, ακριβώς όπως βλέπουμε να συμβαίνει και στο νερό πίσω από την προπέλα ενός πλοίου.

Η αντίσταση μάλιστα του αέρα μεγαλώνει καθώς αυξάνεται και η ταχύτητα της μπάλας (και μάλιστα με το τετράγωνο της ταχύτητας. Δηλαδή όταν διπλασιάζεται η ταχύτητα τετραπλασιάζεται η αντίσταση και έτσι
κάπως η μπάλα φρενάρει).

Αυτό όμως δεν συμβαίνει πάντα. Πάνω από κάποια τιμή της αρχικής ταχύτητας αλλάζει η ροή γύρω από την μπάλα και η αντίσταση μειώνεται! Αρα σε ένα πολύ δυνατό χτύπημα, έχει που έχει ταχύτητα η μπάλα, φρενάρει και λιγότερο, είναι και
πιο αερόμπαλα αυτή η καινούργια και καταλαβαίνουμε το δράμα του τερματοφύλακα. Προσθέστε σε αυτά και το ότι το ένα τέταρτο των οστών του ανθρώπινου σώματος είναι συγκεντρωμένο στα πόδια και με βάση την εξίσωση της
ορμής που είναι μεγαλύτερη όσο πιο μεγάλη είναι η μάζα του κινούμενου σώματος (εδώ αναφερόμαστε στα πόδια του ποδοσφαιριστή) και την ελαστική κρούση με την καλά φουσκωμένη μπάλα, δεν είναι δύσκολο να ξεπεράσουμε μια ταχύτητα ακόμη και 120 χιλιομέτρων την ώρα.

Και με την καινούρια μπάλα, την κάπως πιο ελαφριά, πιο λεία και πιο στρογγυλή, καταλαβαίνουμε γιατί φωνάζουν ήδη ο Κασίγιας και οι άλλοι τερματοφύλακες.

Ο ΤΡΟΜΟΣ ΤΟΥ ΤΕΡΜΑΤΟΦΥΛΑΚΑ
Στο πέναλτι η ομάδα και ο τερματοφύλακας στήνονται μπροστά στο εκτελεστικό απόσπασμα, «στα 11 μέτρα», όπως λέγεται. Γιατί όμως σε αυτή την απόσταση; Από το 1902 ισχύει ότι η μπάλα, στην πιο βαριά από τις ποινές του ποδοσφαίρου, πρέπει
να στηθεί στις 12 γιάρδες, δηλαδή στα 10,97 μέτρα.

Είναι μια απόσταση, όπως θα δούμε, σχετικά καλά διαλεγμένη. Γι ́ αυτό μπορούν να μας διαβεβαιώσουν και η στατιστική και κάποιοι εύκολοι υπολογισμοί. Η ποινή θα έπρεπε να είναι βαριά,
δηλαδή να είναι σχεδόν γκολ, αλλά όχι και εκατό τοις εκατό, για να υπάρχει ενδιαφέρον. Eχουν λοιπόν επιλέξει μια πιθανότητα κοντά στο 75%. Αυτό έχει αποδειχτεί ότι διατηρείται από πολλές στατιστικές μετρήσεις σε πρωταθλήματα υψηλού επιπέδου και διοργανώσεις όπως το Παγκόσμιο και το Ευρωπαϊκό. Μπορεί όμως να επιτευχθεί το ίδιο αποτέλεσμα και από αλλού.

Οταν το τέρμα έχει άνοιγμα 7,32 μέτρα και ύψος 2,44, η επιφάνειά του βγαίνει κοντά στα 18 τετραγωνικά μέτρα. Ενας τερματοφύλακας σε μουντιαλικό επίπεδο είναι περίπου στα 2 μέτρα και το άνοιγμα των χεριών του φθάνει επίσης τα 2 μέτρα, άρα καλύπτει περίπου 4 τετραγωνικά, δηλαδή το 22% της επιφάνειας του τέρματος. Αρα μένει το 78% ακάλυπτο, που είναι κοντά στο 75%. Ίσως θα έπρεπε η μπάλα να στηνόταν περίπου μισό μέτρο πιο πίσω για να είναι τα πράγματα πιο δίκαια. Διότι είναι και ο χρόνος αντίδρασης του τερματοφύλακα που πρέπει να λογαριαστεί. Στα πέναλτι η μέγιστη ταχύτητα της μπάλας φθάνει τα 120-130 χιλιόμετρα την ώρα. Αλλά ο μέσος όρος βγαίνει κάπου 100 χιλιόμετρα την ώρα. Για να διανύσει η μπάλα την απόσταση των 11 μέτρων, χρειάζεται κατά προσέγγιση χρόνο 0,4 δευτερόλεπτα.

Ένας άνθρωπος χρειάζεται 0,2 δευτερόλεπτα για να αντιληφθεί προς το πού κατευθύνεται η μπάλα, άρα του μένουν 0,2 ακόμη για να αντιδράσει. Αλλά η εκτίναξη ως τη γωνία του, που είναι σε απόσταση 3,66 μέτρων με 40 χιλιόμετρα την ώρα ταχύτητα, χρειάζεται χρόνο 0,33 δευτερολέπτων.

Γι ́ αυτό βλέπουμε τους τερματοφύλακες να έχουν από πριν αποφασίσει προς τα πού θα πέσουν. Όσο για τη διαδικασία των 5 πέναλτι, μετά τους αγώνες των ομίλων, όταν πρέπει πάντα να αναδειχτεί κάποιος νικητής, έχουν γίνει μελέτες και με τη θεωρία των πιθανοτήτων και με στατιστικές. Και βγαίνει ότι, αφού στις προπονήσεις έχουν χτυπηθεί άπειρα πέναλτι και έχουν γίνει στατιστικές μελέτες, η καλύτερη στρατηγική είναι το πρώτο πέναλτι να το χτυπάει ο χειρότερος των πέντε παικτών που έχουν
επιλεγεί και να πηγαίνουμε προς τον καλύτερο, δηλαδή τον πιο εύστοχο αλλά και πιο ψύχραιμο, όταν πιθανόν η πίεση έχει ανέβει στα ύψη.

Αφού ανέλυσαν δεκάδες ώρες ποδοσφαίρου καποιοι αθλητικοί επιστήμονες, ένας από τους οποίους ο Ken Bray, κατέληξαν στο συμπέρασμα πως οι κορυφαίοι ποδοσφαιριστές όπως ο Κριστιάνο Ρονάλντο, ο Μέσι ,ο Νειμαρ και Εμπαπε είναι
πολύ καλοί στα μαθηματικά.

ΤΑ ΦΑΟΥΛ
Για τις εκτελέσεις φάουλ από απόσταση 23 μέτρων η μπάλα πρέπει να φύγει από το πόδι του ποδοσφαιριστή με γωνία 16 μοιρών. Για τους δεξιοπόδαρους πρέπει να χτυπηθεί ελαφρά προς τα δεξιά ώστε να πάρει τα φάλτσα και να κατευθυνθεί με
δύναμη προς την εστία. Η αρχική ταχύτητα της μπάλας πρέπει να είναι 95-115 χλμ. / ώρα και να περιστρέφεται με 600 στροφές το λεπτό.

Τα μαθηματικά είναι για όλους
Μια άλλη αρχή στην οποία πιστεύουμε είναι ότι τα μαθηματικά είναι για όλους. Αυτή η αυτονόητη αρχή της υποχρεωτικής εκπαίδευσης σημαίνει ότι σε όλους τους μαθητές, είτε έχουν ή όχι ιδιαίτερη κλίση, είτε ανήκουν σε εθνικές μειονότητες, είτε
έχουν μαθησιακές δυσκολίες κ.ά., το εκπαιδευτικό σύστημα οφείλει να διδάξει τα μαθηματικά και να μη δημιουργηθεί αρνητική στάση προς το μάθημα αυτό. Αυτό το σύνθετο έργο εκτός από το κατάλληλο εκπαιδευτικό υλικό αναφέρεται περισσότερο στον εκπαιδευτικό και τη διδασκαλία που θα πραγματοποιήσει μέσα στην τάξη.

Τα βιβλία των μαθηματικών αλλά και η διδασκαλία των εκπαιδευτικών θα πρέπει να δίνουν σε όλους τους μαθητές ανεξαιρέτως, την ευκαιρία να προβληματιστούν, να ασχοληθούν με ευχάριστες για αυτούς δραστηριότητες και να μάθουν σύμφωνα με την προσωπική τους υποδομή και ρυθμούς.

ΠΟΔΟΣΦΑΙΡΟ ΚΑΙ ΜΑΘΗΜΑΤΙΚΑ ΣΥΝΥΠΑΡΧΟΥΝ
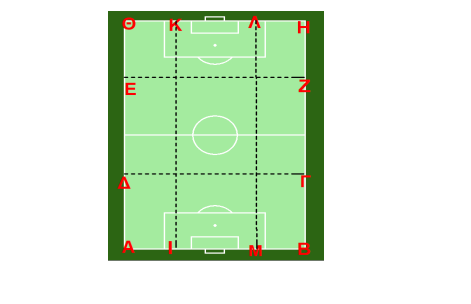
Ακολουθεί προσωπική μελέτη σχετικά με τα συστήματα παιχνιδιού Το γήπεδο ποδοσφαίρου που παίζεται το ποδόσφαιρο είναι ορθογώνιο. Το μήκος του είναι από 90 μέχρι 120 μέτρα και το πλάτος του από 45 μέχρι 90 μέτρα. Από την τελική γραμμή κάθε περιοχής και στη μέση της υπάρχουν δύο κάθετα δοκάρια, που απέχουν μεταξύ τους 7,32 μ. και συνδέονται μ’ ένα οριζόντιο δοκάρι που έχει ύψος απ’ το έδαφος 2,44 μ. Αυτό είναι το τέρμα.

Το γήπεδο ποδοσφαίρου το χωρίζουμε σε ίσες ζώνες στο μήκος και στο πλάτος. ∆ημιουργούμε δηλαδή έξι (6) ορθογώνια. Η επιτιθέμενη πλευρά κινείται από αριστερά στα δεξιά. Το ορθογώνιο ΑΒΓ∆ αποτελεί την αμυντική γραμμή, το Γ∆ΕΖ την μεσαία γραμμή και το ΕΖΗΘ την επιθετική γραμμή οι περισσότερες ενέργειες που αφορούν την στρατηγική στην άμυνα, στο κέντρο και την επίθεση εκδηλώνονται σ’ αυτές τις ζώνες. Εξίσου σημαντικά είναι και τα κεντρικά και πλάγια τμήματα. Το ορθογώνιο ΑΙΚΘ αποτελεί το αριστερό πλάγιο τμήμα, το ΙΜΛΚ το μέσο τμήμα και το ΜΛΗΒ το
δεξιό πλάγιο τμήμα

Α. Σύστημα 4-2-4

Ονομάζεται έτσι επειδή τέσσερις παίκτες καλύπτουν την αμυντική γραμμή, δύο παίκτες την μεσαία γραμμή και τέσσερις την επιθετική. Ας βρούμε πόσες επιλογές πάσας έχουν οι 10 παίκτες, εκτός του τερματοφύλακα . Ο κάθε παίκτης μπορεί να δώσει πάσα στους υπόλοιπους 9 άρα 9 πάσες δηλάδη συνολικά 9*10= 90 πάσες. Αν επιλέξουμε ως ανώτατο όριο της πάσας, τα 40 μέτρα, γιατί όσο πιο μακριά “ταξιδεύει η μπάλα, τόσο πιο πιθανό είναι να κοπεί από αντίπαλο, και υποθέσουμε πως όλες οι πάσες είναι την εμβέλεια τότε θα έχουμε :

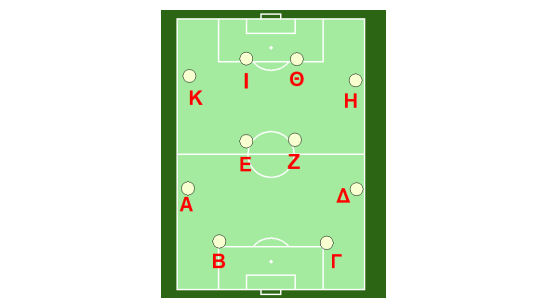
Ο Α παίκτης έχει : 4 επιλογές ( στο Β, Γ, Ε, Ζ)
Ο Β παίκτης έχει : 5 επιλογές ( Α, Γ, ∆, Ε, Ζ)

Ο Γ παίκτης έχει : 5 επιλογές ( Α, Β, ∆, Ε. Ζ)
Ο ∆ παίκτης έχει : 4 επιλογές ( Γ, Β, Ε, Ζ)
Ο Ε παίκτης έχει : 9 επιλογές ( Α, Β, Γ, ∆, Ζ, Η, Θ, Ι ,Κ)
Ο Ζ παίκτης έχει : 9 επιλογές ( Α, Β, Γ, ∆, Ε, Η, Θ, Ι, Κ, )
Ο Η παίκτης έχει : 4 επιλογές ( Ε, Ζ, Θ, Ι )
Ο Θ παίκτης έχει : 5 επιλογές ( Ε, Ζ, Η, Ι, Κ)
Ο Ι παίκτης έχει : 5 επιλογές ( Ε, Ζ, Η, Θ, Κ )
Ο Κ παίκτης έχει : 4 επιλογές (Ε, Ζ, Θ, Ι)
Αμυντικοί : 4+5+5+4= 18
Μέσοι : 9+9= 18
Επιθετικοί : 4+5+5+4= 18

Συνολικά 54 διαθέσιμες πάσες σε αυτό το σύστημα.
Από αυτές μόνο 4+5+5+4=18 πάσες φτάνουν στην γραμμή επίθεσης δηλαδή
ποσοστό 18/54*100 =33,33 %

Β. Σύστημα 4-3-3

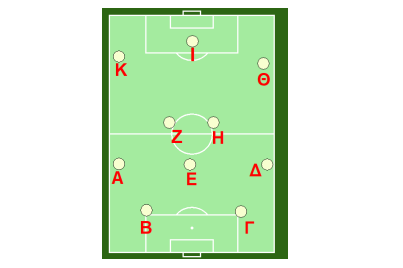
Με όμοιο τρόπο, οι επιλογές πάσας 40 μέτρων σε αυτό το σύστημα είναι:
Ο Α παίκτης έχει : 4 επιλογές ( Β, Γ, Ε, Ζ)
Ο Β παίκτης έχει : 6 επιλογές ( Α, Γ, ∆, Ε, Ζ, Η)
Ο Γ παίκτης έχει : 6 επιλογές ( Α, Β, ∆, Ε. Ζ, Η)
Ο ∆ παίκτης έχει : 4 επιλογές ( Γ, Β, Ε, Ζ)
Ο Ε παίκτης έχει : 9 επιλογές ( Α, Β, Γ, ∆, Ζ, Η, Θ, Ι ,Κ)
Ο Ζ παίκτης έχει : 7 επιλογές ( Α, Β, Ε, Η, Θ, Ι, Κ, )
Ο Η παίκτης έχει : 7 επιλογές ( Γ,Δ, Ε, Ζ, Θ, Ι, Κ )
Ο Θ παίκτης έχει : 4 επιλογές ( Ε, Ζ, Η, Ι, )
Ο Ι παίκτης έχει : 5 επιλογές ( Ε, Ζ, Η, Θ, Κ )
Ο Κ παίκτης έχει : 4 επιλογές (Ε, Ζ, Η, Ι)
Αμυντικοί : 4+6+6+4= 20
Μέσοι : 7+9+7= 23
Επιθετικοί : 4+5+4= 13

Συνολικά 56 πάσες με ποσοστό 13/56*100= 23,2% στη γραμμή επίθεσης.

Γ. Σύστημα 4-4-2

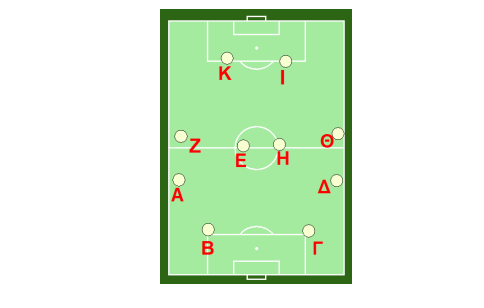
Οι επιλογές πάσας είναι :
Ο Α παίκτης έχει : 5 επιλογές ( Β, Γ, Ε, Ζ, Η )
Ο Β παίκτης έχει : 7 επιλογές ( Α, Γ, ∆, Ε, Ζ, Η, Θ)
Ο Γ παίκτης έχει : 7 επιλογές ( Α, Β, ∆, Ε. Ζ, Η , Θ)
Ο ∆ παίκτης έχει : 5 επιλογές ( Γ, Β, Ε, Η, Θ)
Ο Ε παίκτης έχει : 9 επιλογές ( Α, Β, Γ, ∆, Ζ, Η, Θ, Ι, Κ)
Ο Ζ παίκτης έχει : 7 επιλογές ( Α, Β, Ε, Η, Θ, Ι, Κ,)
Ο Η παίκτης έχει : 9 επιλογές ( Γ,Δ, Ε, Ζ, Θ, Ι, Κ )
Ο Θ παίκτης έχει : 7 επιλογές ( Α, Β, Ε, Η, Θ, Ι, Κ)
Ο Ι παίκτης έχει : 5 επιλογές ( Ε, Ζ, Η, Θ, Κ )
Ο Κ παίκτης έχει : 5 επιλογές (Ε, Ζ, Η, Ι, Θ )
Αμυντικοί : 5+7+7+5= 24
Μέσοι : 7+9+9+7= 32
Επιθετικοί : 5+5=10
Συνολικά 66 πάσες με ποσοστό 10/66*100= 15,15 % στην γραμμή επίθεσης.

∆. Σύστημα 4-5-1

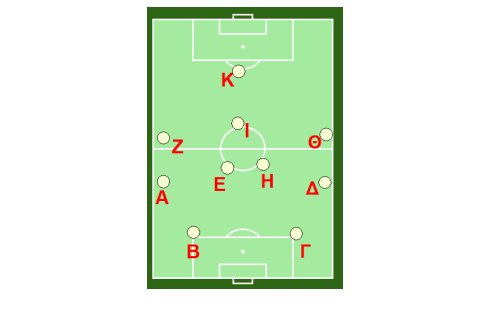
Οι επιλογές πάσας είναι :
Ο Α παίκτης έχει : 5 επιλογές ( Β, Ε, Η, Ζ, Ι )
Ο Β παίκτης έχει : 7 επιλογές ( Α, Γ, ∆, Ε, Ζ ,Η, Θ)
Ο Γ παίκτης έχει : 7 επιλογές ( Α, Β, ∆, Ε. Ζ, Η ,Θ)
Ο ∆ παίκτης έχει : 5 επιλογές ( Γ, Ι , Ε, Η, Θ)
Ο Ε παίκτης έχει : 9 επιλογές ( Α, Β, Γ, ∆, Ζ, Η, Θ, Ι, Κ)
Ο Ζ παίκτης έχει : 5 επιλογές ( Α, Ε, Η, Ι, Κ,)
Ο Η παίκτης έχει : 9 επιλογές ( Α, Β, Γ, ∆, Ζ, Ε, Θ, Ι, Κ)
Ο Θ παίκτης έχει : 5 επιλογές ( Δ, Η, Ε, Ι, Κ)
Ο Ι παίκτης έχει : 5 επιλογές ( Ε, Ζ, Η, Θ, Κ )
Ο Κ παίκτης έχει : 5 επιλογές (Ε, Ζ, Η, Ι, Θ )
Αμυντικοί : 5 +7+7+5=24
Μέσοι : 5+9+5+9+5=33
Επιθετικοί : =5
Συνολικά 62 πάσες με ποσοστό 5/62*100= 8% στην επιθετική γραμμή.

Παρατηρούμε ότι το σύστημα 4-4-2 ( 66 μεταβιβάσεις ) είναι το καλύτερο , ενώ το
4-2-4 ( 54 μεταβιβάσεις) είναι το χειρότερο.

Στο 4-4-2 κάθε παίκτης έχει περισσότερες επιλογές, καθώς υπάρχουν 66/100= 6,6=7 συμπαίκτες σε απόσταση για πάσα, ενώ στο 4-2-4 υπάρχουν 54/10= 5,4=5 παίκτες, κατά μέσο όρο, σε απόσταση για πάσα.

Το κέντρο είναι η περιοχή όπου παρατηρείται συνήθως ο μεγαλύτερος συνωστισμός, καθώς όλη η κυκλοφορία της μπάλας, οι πάσες από την άμυνα στην επίθεση και αντίστροφα, περνούν από το χώρο του κέντρου. Από αυτήν την άποψη, το έργο που
ανατίθεται στους μμέσους, δηλαδή πόση δουλειά διεκπεραιώνουν παραλαμβάνοντας και “μοιράζοντας” την μπάλα, αποτελεί καθοριστικό παράγοντα σε κάθε αγωνιστικό σύστημα.
Για να δούμε λοιπόν πόσες πάσες ενός αγώνα( πάσες προς τα εμπρός, προς τα πίσω και από παίκτη σε παίκτη) περνούν από το κέντρο σε κάθε αγωνιστικό σύστημα.

Στα 4-2-4 έχουμε : (18/2)/54*100= 16,66= 17% σε κάθε μέσο παίκτη, πολύ
απαιτητικό, γι’ αυτό το σύστημα αυτό έχει εγκαταλειφθεί.
Στο 4-3-3 έχουμε : (23/3)/56*100= 14% σε κάθε μμέσο παίκτη.
Στο 4-4-2 έχουμε : (32/4)/66*100 = 12% σε κάθε μέσο παίκτη.
Στο 4-5-1 έχουμε : (33/5)/62*100=11% σε κάθε μέσο παίκτη.

Άραγε ποιο σύστημα είναι ανώτερο από τα άλλα; Η απάντηση δεν είναι και τόσο προφανής. Πολλά εξαρτώνται από τον βαθμό στον οποίο επηρεάζεται το ποδόσφαιρο από τις στατιστικές πιθανότητες. Ίσως σε τελική ανάλυση, να είναι οι παίκτες που
κάνουν το σύστημα και όχι το αντίθετο.

Το άθλημά με τους περισσότερους φίλους στον κόσμο, συναντά την επιστήμη. Ή πιο σωστά, η επιστήμη με τα σύγχρονα μέσα που διαθέτει κατορθώνει να μελετήσει τα ενδότερα του δημοφιλέστερου αθλήματος στον κόσμο του ποδοσφαίρου.